Logica Matematica: MAPAS DE KARNAUGH

El mapa de Karnaugh es un método gráfico que se utiliza para simplificar una ecuación lógica para convertir una tabla de verdad a su circuito lógico correspondiente en un proceso simple y ordenado. Aunque un mapa de Karnaugh (que de aquí en adelante se abreviará como mapa K) se puede utilizar para resolver problemas con cualquier numero de variables de entrada, su utilidad practica se limita a seis variables. El siguiente análisis se limitara a problemas de hasta cuatro entradas , ya que los problemas con cinco y seis entradas son demasiado complicados y se resuelven mejor con un programa de computadora.

Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadricula de 4 × 4.

La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas. Por ejemplo, la celda en la esquina superior izquierda del mapa es 0, porque el resultado de la función es ƒ = 0 cuando A = 0, B = 0, C = 0, D = 0. De igual manera, la esquina inferior derecha es 1 porque el resultado de la función es ƒ = 1 cuando A = 1, B = 0, C = 1, D = 0.

Una vez construido el mapa de Karnaugh, la siguiente tarea es la de seleccionar conjuntos de términos de manera que se obtenga el menor número de términos posible. Estos términos se seleccionan formando grupos de rectángulos cuyas areas sean potencia de 2 (ej. 1, 2, 4, 8, ...) tratando de agrupar el mayor número de términos posible.

Que términos seleccionar van dependiendo de como se quiera realizar la simplificación, puesto que esta puede realizarse por minitérminos o por maxitérminos.

MINITERMINOS

Para una función booleana de

n

variables

x 1,... x n

, un producto booleano en el que cada una de las

n

variables aparece una sola vez (negada o sin negar) es llamado minitérmino. Es decir, unminitérmino es una expresión lógica de n variables consistente únicamente en el operador conjunción lógica (AND) y el operador complemento o negación (NOT).

Por ejemplo,

a b c

a b' c

a b c'

son ejemplos de minterms para una función booleana con las tres variables

a

b

c

Indexando minitérminos

En general, uno asigna a cada minterm (escribiendo las variables que lo componen en el mismo orden), un índice basado en el valor binario del minterm.

Un término negado, como

a'

es considerado como el número binario 0 y el término no negado

a

es considerado como un 1.

Por ejemplo, se asociaría el número 6 con

a b c'

, y nombraríamos la expresión con el nombre

m 6

. Entonces

m 0

de tres variables es

a' b' c'

m 7

debería ser

a b c

al ser

111 (2

Se puede observar que cada minterm solo devuelve verdadero, (1), con una sola entrada de las posibles.

Por ejemplo, el minitérmino 5,

a b' c

es verdadero solo cuado a y c son ciertos y b es falso - la
entrada a = 1, b = 0, c = 1 da resultado 1.

Función equivalente

Si tenemos una tabla de verdad de una función lógica: f(a,b), es posible escribir la función como "suma de productos". Por ejemplo, dada la tabla de verdad.

$\begin{array}{|c||c|c||c|} \hline n & a & b & f(a,b) \\ \hline 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 2 & 1 & 0 & 0 \\ 3 & 1 & 1 & 1 \\ \hline \end{array}$

Observamos que las filas con resultado '1 son la primera y la cuarta, entonces podremos escribir f como la suma de los minitérminos:

f (a, b) = m 0 + m 3

Si queremos verificar esto:

f (a, b) = m 0 + m 3 = (a' b') + (a b)

tendremos que la tabla de verdad de la función, calculándola directamente, será la misma.

Esta expresión aplicada a interruptores seria el de la figura, se puede ver que hay dos ramas, en la superior dos interruptores inversos: a’ y b’ puestos en serie, lo que es equivalente a a’b’, en la inferiores directos: a y b también en serie que es equivalente a ab, estos dos circuitos puestos en paralelo resultan a’b’ + ab.

Maxitérminos

Un maxitérmino es una expresión lógica de n variables que consiste únicamente en la disyunción lógica y el operador complemento o negación. Los maxterms són una expresión dual de los minitérminos. En vez de usar operaciones AND utilizamos operaciones OR y procedemos de forma similar.

Por ejemplo, los siguientes términos canónicos son maxitérminos:

a + b' + c

a' + b + c

[editar]Dualización

$\begin{array}{|c|c l|c l||c|c|c|} \hline n & M & & m & & a & b & c \\ \hline 0 & M_0= & a + b + c & m_0= & a'b'c'& 0 & 0 & 0 \\ 1 & M_1= & a + b + c'& m_1= & a'b'c & 0 & 0 & 1 \\ 2 & M_2= & a + b'+ c & m_2= & a'b c'& 0 & 1 & 0 \\ 3 & M_3= & a + b'+ c'& m_3= & a'b c & 0 & 1 & 1 \\ 4 & M_4= & a'+ b + c & m_4= & a b'c'& 1 & 0 & 0 \\ 5 & M_5= & a'+ b + c'& m_5= & a b'c & 1 & 0 & 1 \\ 6 & M_6= & a'+ b'+ c & m_6= & a b c'& 1 & 1 & 0 \\ 7 & M_7= & a'+ b'+ c'& m_7= & a b c & 1 & 1 & 1 \\ \hline \end{array}$

El complemento de un minterm es su respectivo maxitérmino. Esto puede ser fácilmente verificado usando la Ley de De Morgan. Por ejemplo:

m 1' = M 1

(a' b)' = a + b'

[editar]Indexando maxitérminos

Para indexar maxitérminos lo haremos justo de la forma contraria a la que seguimos con los minterms. Se asigna a cada maxterm un índice basado en el complemento del número binario que representa (otra vez asegurándonos que las variables se escriben en el mismo orden, usualmente alfabético). Por ejemplo, para una función de tres variables f(a,b,c) podemos asignar

M 6

(Maxitérmino 6) al maxitérmino:

a' + b' + c

. De forma similar

M 0

de tres variables debería ser

a + b + c

M 7

a' + b' + c'

Se puede ver fácilmente que un maxitérmino sólo da como resultado un cero para una única entrada de la función lógica. Por ejemplo, el maxitérmino 5,

a' + b + c'

, es falso solo cuando a y c son ciertos y b es falso - la entrada a = 1, b = 0, c = 1 da como resultado un cero.

[editar]Función equivalente

$\begin{array}{|c||c|c||c|} \hline n & a & b & f(a,b) \\ \hline 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 2 & 1 & 0 & 0 \\ 3 & 1 & 1 & 1 \\ \hline \end{array}$

Si tenemos una tabla de verdad de una función lógica, f(a,b), es posible escribir la función como "producto de sumas". Por ejemplo, dada la tabla de verdad.

Observamos que las filas que tiene como salida un 0 son la segunda y la tercera, entonces podemos escribir f como un producto de maxitérminos

M 1 M 2

Si queremos verificar esto:

f (a, b) = (a + b')(a' + b)

tendremos que la tabla de verdad de la función, calculándola directamente, será la misma.

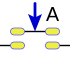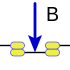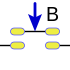La aplicación en un circuito de interruptores, es el del esquema, donde se puede ver los dos interruptores superiores a y a', y los inferiores b' y b.

En primer lugar tenemos puestos en paralelo a y b', lo que seria a+b', y a continuación, a' y b en paralelo que seria a'+b, estos dos circuitos parciales puestos en serie son equivalentes a (a+b')(a'+b), las distintas combinaciones de a y b, corresponden, como se puede ver a la tabla de verdad.

Este circuito esta cerrado solo en dos de las cuatro combinaciones posibles: a b con los interruptores en esta posición se conecta la entrada con la salida y a’ b’ que también cierra circuito, para las otras combinaciones el circuito esta abierto.